
Algorithmique
Introduction et concepts élémentaires
Faculté des sciences
- Bases de l'Algorithmique
- Introduction
- Types, variables et opérateurs
- Instructions structurées
- Les tableaux
- Tableaux unidimensionnels
- Tableaux bidimensionnels
- Les fonctions
Qu'est-ce qu'un algorithme ?
Un algorithme est une suite d'actions exécutées en un temps fini. Ces actions s'appliquent à des données pour les transformer et/ou créer de nouvelles données.
Processus systématique de résolution d'un problème
C'est une suite finie et non-ambiguë d'opérations
Les données auxquelles s'appliquent un algorithme forment l'entrée de l'algorithme.
Les données produites par un algorithme forment la sortie de l'algorithme.
Pour donner une image...
La recette du gâteau au chocolat- De quels ingrédients avez-vous besoin ?
- Comment s'y prendre ?
- Que veux-t-on obtenir au final ?
Pour donner une image...
La recette formalisée en algorithme- entrée : oeufs, farine, yaourts, chocolat, sucre, beurre...
- sortie : un beau gâteau au chocolat
- algorithme : les instructions qui permettent de transformer les ingrédients (entrée) en gâteau au chocolat (sortie)
L'algorithmique en informatique
Un algorithme est là pour résoudre un problème.
Plus précisément, il va permettre à la machine de le résoudre !
Note : il peut y avoir plusieurs solutions pour atteindre le même résultat
Concevoir un algorithme pour résoudre un problème
- l'énoncé du problème identifie les données en entrée et celles attendues en sortie
- concevoir un algorithme c'est trouver les étapes pour obtenir la sortie à partir de l'entrée
- ...et ceci de manière infaillible !
L'algorithmique en informatique
Exemple élémentaireEtant donné un triangle de dimensions a, b, c. Ce triangle est-il rectangle sachant que c est le plus grand côté ?
- entrée : 3 nombres réels désignés par a, b, c
- sortie : 2 réponses possibles, "c'est un triangle rectangle" ou "ce n'est pas un triangle rectangle"
- l'algorithme :
-
- calculer toto = a2 + b2
- calculer tutu = c2
- si toto est égal à tutu, répondre "c'est un triangle rectangle"
- sinon répondre "ce n'est pas un triangle rectangle"
Définition informelle
L'algorithmique est un ensemble de concepts qui permettent de décrire un raisonnement de sorte à le rendre reproductible par tous et surtout par une machine
Quels concepts ?
- les concepts permettant la représentation des données la mémoire d'un ordinateur
- les concepts permettant de donner des instructions, des ordres à un ordinateur
L'algorithmique c'est puissant
Le nombre de concepts à connaître n'est pas très important
- types, variables, opérateurs...
- instructions structurées, données structurées
- fonctions...
Et pourtant en les combinant, on peut décrire des raisonnements très complexes.
L'algorithmique est mère de tous les langages de programmation
C, C++, Java, Javascript, PHP, Python, Perl, C#... Tous les langages mettent en oeuvre les concepts de l'algorithmique.
L'algorithme permet de décrire des raisonnements. Les langages permettent de les programmer sur machine.
Réfléchir avant d'agir
La conception d'un algorithme précède toujours sa programmation sur machine ! Ne jamais vouloir faire les deux à la fois !
Dans ce cours, nous utiliserons c++
C'est différent de Scratch
On ne peut pas éxecuter directement le programme
Nous procéderons par étapes :
- Concevoir l'algorithme
- Ecrire le programme source en langage évolué (ici, c++)
- Phase de compilation (traduction en langage machine)
- On obtient un programme exécutable
-
Un exemple en C++

int main()
{
int a = rand()%10 +1;
int b = rand()%10+1;
int reponse;
std::cout << "Quel est le résultat ?";
std::cin >> reponse;
if (a*b == reponse)
std::cout << "Gagné" << std::endl;
else
{
std::cout << "Perdu, la réponse était : ";
std::cout << a*b << std::endl;
}
}
Conseils et conventions
- Définir precisément le problème
- Déterminer une méthode de résolution et choisir une représentation des données
- Etre méthodique et rigoureux (la machine ne comprend pas les approximations)
-
- Bases de l'Algorithmique
- Introduction
- Types, variables et opérateurs
- Instructions structurées
- Les tableaux
- Tableaux unidimensionnels
- Tableaux bidimensionnels
- Les fonctions
Les types de données
Un algorithme manipule des données- qui peuvent être simples : un nombre, un caractère...
- ou plus complexes : une image, un son, des personnes...
Mais sur une machine...
- Où peut-on écrire des données ?
- Que peut-on lire/écrire sur ces supports ?
Un problème de représentation
Comment représenter (écrire ou lire) un nombre, une image, etc... sur un support qui est une succession de 0 et de 1 ?
Impossible de raisonner au niveau du support physique ! Il faut se placer à un niveau d'abstraction supérieur grâce à la notion de type.
Qu'est-ce qu'un type ?
DéfinitionUn type permet d'identifier la nature d'une donnée. Par exemple s'il s'agit d'un entier ou bien d'un caractère etc...
Pourquoi est-ce important pour nous ?
Vous préférez raisonner sur des entiers, des lettres... ou bien directement avec leur équivalent binaire ?
Pourquoi est-ce important pour la machine ?
A partir du type d'une donnée, la machine sera capable de définir l'espace mémoire qui lui est nécessaire ainsi que son code binaire
Les types élémentaires de données
int : le type entier (integer)
Il indique que la donnée manipulée est un chiffre ou un nombre entier. Par exemple 1, 123, -2, -44
float, double : le type nombre réel (floating number)
Il indique que la donnée manipulée est un nombre réel. Par exemple 2.6, -5.9, 1024.0
Note
: la différence entre float et double réside dans le nombre de chiffres
représentables après la virgule. Les nombres de type double sont plus
précis mais prennent aussi plus de place en mémoire (le double en
général)
Les types élémentaires de données
boolean : le type booléen
Il désigne une donnée à 2 valeurs possibles : true ou false
char : le type caractère
Il indique que la donnée manipulée est une lettre ou un symbole. Par exemple 'a', 'A', 'b', 'B', ... 'y', 'Y', 'z', 'Z' sont des caractères. ':', '?', '$'... le sont aussi.
Un caractère s'écrit toujours en utilisant des guillemets simples. Attention à ne pas confondre le chiffre 9 par exemple, avec le caractère '9' !
Les types (moins) élémentaires de données
String : le type chaîne de caractères
Il indique que la donnée manipulée est une suite de caractères. Donc un mot, une phrase ou un texte.
Par exemple "Algorithmique", "Info1" sont des chaînes de caractères. Mais aussi "" qui est la chaîne de caractères vide.
Une chaîne de caractères s'écrit toujours entre guillemets doubles. Attention à ne pas confondre la chaîne "123.4" avec le nombre réel 123.4 par exemple !
Les types c'est pratique,
mais insuffisant
Un type permet d'identifier la nature d'une donnée. Pour autant il ne permet pas de désigner une donnée en elle même !
Par exemple les nombres 28 et 62 ne sont pas distingable par leur type : ce sont tous les deux des entiers.
Comment manipuler une donnée si on ne sait pas l'identifier ? C'est là qu'intervient la notion de variable...
Les variables
Qu'est-ce donc ?- une variable permet de stocker une donnée
- elle possède un nom utilisé pour désigné la donnée contenue
- elle possède un type et ne peut contenir que des données de ce type
- au cours du temps une variable peut recevoir des données différentes
Note : tant qu'elles sont du même type que la variable !
L'image de la boîte
Une variable peut être comparée à une boîte dans laquelle on range des affaires (des données)
Chaque boîte est étiquettée (le nom de la variable)
Chaque boîte possède une forme qui lui permet uniquement de recevoir des données de cette forme (même type)
Attention, en Scratch, les variables n'ont pas de type. En C++, les types sont indispensables !
Déclaration et affectation
de variables
Dans un programme, un algorithme, on passe son temps à jongler avec des variables pour utiliser des données issues du disque, d'une saisie au clavier... ou stocker de nouvelles données que l'on aura calculées.
Ce n'est possible qu'en utilisant des variables
Et pour utiliser une variable, il faudra observer 2 étapes :
- Déclarer la variable
- Affecter la variable
Déclaration d'une variable
Déclarer une variable c'est lui donner un nom et indiquer son type.
C'est son "acte de naissance", vouloir utiliser une variable non déclarée c'est vouloir utiliser quelque chose qui n'existe pas !
Côté machine
En déclarant une variable, vous commandez à la machine de réserver un espace mémoire adéquat pour stocker une donnée du type choisi. Vous lui dites aussi que vous ferez référence à cette donnée par le nom de la variable.
Déclaration d'une variable en C++
- indiquer son type
- puis son nom
// Déclaration d'une variable de type entier et nommée alpha
int alpha;
// Déclaration d'une variable de type caractère et nommée lettre
char lettre;
// Déclaration d'une variable de type réel et nommée nombre
float nombre;
// Déclaration d'une variable de type booléen et nommée ouinon
bool ouinon;
Notons au passage :
- le point-virgule : il marque la fin de toute instruction. Et la déclaration d'une variable en est une.
- le double slash // : Il indique un commentaire sur une seule ligne. Un commentaire sera ignoré par la machine. Il est là pour expliquer le code, l'algorithme, aux personnes qui auront à lire ou relire ce code.
Du coté de la machine
En pratique, déclarer une variable revient à réserver de l'espace en mémoire
La machine "interprete" la variable en une adresse mémoire
Le type de la variable indique comment lire et dechiffrer les 0 et les 1

Affectation d'une variable
Après sa déclaration, une variable est une "boîte vide", elle ne contient pas de valeur.
Pire elle peut contenir n'importe quoi, selon ce qui se trouvait avant dans la zone mémoire réservée par la machine pour la variable.
Affecter une variable c'est y stocker une valeur, tout simplement. On parle d'initialisation pour la première valeur affectée à une variable. Toujours initialiser ses variables.
Affectation d'une variable en C++
// Déclaration d'une variable de type entier et nommée alpha
int alpha;
// Initialisation de la variable alpha avec le nombre 18
alpha = 18;
// Déclaration d'une variable de type caractère et nommée lettre
char lettre;
// Initialisation de la variable lettre avec le caractère 'z'
lettre = 'z';
// Autre syntaxe possible, plus concise mais totalement équivalente
/* Déclaration d'une variable de type entier
et nommée alpha et initialisée à 18 */
int alpha = 18;
/* Déclaration d'une variable de type caractère
et nommée lettre et initialisée à 'z' */
char lettre = 'z';Notons au passage :
- /* ... */ : Il indique un commentaire sur une ou plusieurs lignes. Comme tout commentaire, il sera ignoré par la machine.
Affectation par recopie
Le contenu d'une variable peut être aussi recopié dans une autre.
// Déclaration des variables
int toto; // toto, variable de type entier et non initialisée
int tutu = 123;// tutu, variable de type entier initialisée à 123
// Corps du programme
toto = tutu; // recopie du contenu de tutu dans toto
std::cout << toto ;// affiche le contenu de toto sur la sortie standardNotons au passage :
- la structure d'un programme : prenez l'habitude de déclarer d'abord toutes les variables utiles à votre programme. Ensuite viennent les instructions à proprement parler : le corps du programme.
- std::cout : Il s'agit de l'instruction
commandant à la machine d'afficher textuellement à l'écran le contenu de
la variable donnée après le symbole << . Equivalent a

Affecter le résultat
d'une expression
Une expression est le plus souvent un calcul dont le résultat peut être affecté à une variable. C'est même très souhaitable si on veut en garder la trace !
// Déclaration des variables
int toto; // toto, variable de type entier et non initialisée
// Instructions du programme
toto = 12 + 3; // toto est initialisé à 15Notons au passage :
- la machine évaluera d'abord l'expression 12+3, puis affectera le résultat à toto.
- de manière générale, la machine évalue toujours en premier le terme de droite (ici 12+3) avant d'affecter le résultat au terme de gauche (ici toto)
- attention à la cohérence des types ! Que dire de l'exemple ci-dessus si toto était de type booleén ?
Erreurs :
Les grands classiques
Confondre le nom d'une variable avec sa valeur
// Déclaration des variables
char o; // o, variable de type caractère et non initialisée
String mot; // mot, variable de type chaîne et non initialisée
// Instructions du programme
o = 'o';// la variable o est initialisée avec le caractère 'o'
mot = "mot";// la variable mot est initalisée avec la chaîne "mot"Moralité :
- n'ajoutez pas à la confusion, choisissez intelligemment les noms de vos variables.
- le nom d'une variable doit autant que possible évoquer l'usage qu'on lui réserve.
Interagir avec le monde exterieur
Afficher des données
// Déclaration des variables
int a = 12; // a, variable de type entier initialisée a 12
std::cout << a << std::endl; // Affiche vers la sortie le contenu de la variable a et revient à la ligneNotes :

- std::cout est l'instruction commandant à la machine d'afficher textuellement à l'écran l'expression donnée après le symoble << (ici, le contenu de la variable a).
- std::cout représente la sortie (cout) standard (ici l'écran)
- std::endl matérialise un retour à la ligne
- Plusieurs expressions, séparées par des << peuvent s'enchainer sur une même ligne.
Astuce : Notez le sens des chevrons (<<) qui
Interagir avec le monde exterieur
Recevoir des données
// Déclaration des variables
int a ; // a, variable de type entier non initialisée
std::cout << "Entrez la valeur de a "; // Affiche vers la sortie le message
std::cin >> a ; // Attends que l'utilisateur entre une valeur et l'affecte à aNotes :

- std::cin est l'instruction commandant à la machine d'attendre une valeur entrée au clavier et de l'affecter à la variable suivant les chevrons >> (ici, la variable a).
- Plusieurs variables, séparées par des >> peuvent recevoir des valeurs successives séparées par des espaces ou retour à la ligne.
Astuce : Notez le sens des chevrons (>>) qui
Les opérateurs
Un opérateur permet de faire... une opération ! Ceci étant, on ne peut pas faire n'importe quelle opération avec n'importe quelle donnée. On distinguera :
- les opérateurs arithmétiques
- les opérateurs de comparaison
- les opérateurs logiques
Les opérateurs arithmétiques
Ils s'appliquent à des nombres de type int, float ou double :
+ : addition
- : soustraction
* : multiplication
/ : division
% : modulo. 12%5 signifie le reste de la division (entière) de 12 par 5. Soit ici 2.
Les opérateurs arithmétiques
L'opérateur + s'applique aussi à des chaînes mais la signification est autre. Il s'agît alors de l'opérateur de concaténation : ajouter les chaînes l'une à la suite de l'autre.
// Déclaration des variables
string mot1 = "Hello ";
string mot2 = "World ! ";
// Instructions du programme
string phrase1 = mot1+mot2;
Erreurs : les grands classiques
La division n'est pas tout à fait la même selon si on l'applique à des entiers ou des réels.
Avec des réels : division "normale".
Avec des entiers : division entière ou euclidienne.
// Déclaration des variables
int toto;
float tutu;
// Instructions du programme
toto = 10 / 3;
tutu = 10.0 / 3.0;
/*
Notez bien la cohérence des types !
Que vaut toto ?
Que vaut tutu ?
Indice : leurs valeurs sont différentes
*/Exemple
Ecrire un algorithme qui demande à l'utilisateur de saisir un nombre de semaines au clavier et affiche en retour à l'écran le nombre de secondes équivalent
// Déclaration des variables
int nb_semaines, nb_jours, nb_secondes;
// Instructions du programme
std::cout << "Saisir un nombre de semaines";
std::cin >> nb_semaines ;
nb_jours = nb_semaines * 7;
nb_secondes = nb_jours * 24 * 60 * 60;
std::cout << "Le nombre équivalent de secondes est : " << nb_secondes << std::endl;Les opérateurs de comparaison
Ils permettent de comparer des données de même type.
Le résultat d'une comparaison est un booléen (true ou false).
Ils ne s'appliquent pas à des données de type String et non pas tous du sens avec des données de type booléen.
Inférieur strict : <
Teste si une valeur est strictement inférieure à une autre
// Déclaration des variables
boolean comp1, comp2;
// Instructions du programme
comp1 = 4 < 3;// comp1 contiendra false
comp2 = 'e' < 'z';
// comp2 contiendra trueNotons au passage :
- on pourrait aussi comparer deux variables de même type, la comparaison s'effectue alors sur les valeurs qu'elles contiennent.
- la comparaison entre caractères se fait selon l'ordre alphabétique. En fait c'est la valeur des codes ascii que la machine compare.
Supérieur strict : >
Teste si une valeur est strictement supérieure à une autre
// Déclaration des variables
boolean comp1, comp2;
// Instructions du programme
comp1 = 4 > 3;// comp1 contiendra true
comp2 = 'e' > 'z';
// comp2 contiendra falseInférieur ou égal : <=
Teste si une valeur est inférieure ou égale à une autre
// Déclaration des variables
boolean comp1, comp2;
// Instructions du programme
comp1 = 3 <= 3;// comp1 contiendra true
comp2 = 'e' <= 'z';
// comp2 contiendra trueSupérieur ou égal : >=
Teste si une valeur est supérieure ou égale à une autre
// Déclaration des variables
boolean comp1, comp2;
// Instructions du programme
comp1 = 3 >= 3;// comp1 contiendra true
comp2 = 'e' >= 'z';
// comp2 contiendra falseEgalité : ==
Teste si deux valeurs sont identiques
// Déclaration des variables
boolean comp1, comp2;
// Instructions du programme
comp1 = 3 == 3;// comp1 contiendra true
comp2 = 'e' == 'z';
// comp2 contiendra false
// Attention à ne pas confondre avec = (affectation)Différence : !=
Teste si deux valeurs sont différentes
// Déclaration des variables
boolean comp1, comp2;
// Instructions du programme
comp1 = 3 != 3;// comp1 contiendra false
comp2 = 'e' != 'z';
// comp2 contiendra trueLes opérateurs logiques

Les opérateurs logiques sont issus de l'algèbre de Boole. Un monde où vivent des variables qui ne peuvent posséder que deux états : 0 ou 1.
Les opérateurs logiques s'appliquent uniquement à :
- des valeurs ou variables de type booléen
- des expressions dont le résultat est un booléen
L'opérateur logique AND : &&
| A | B | A && B |
| true | true | true |
| true | false | false |
| false | true | false |
| false | false | false |
Le résultat est true ssi les deux opérandes A et B valent true.
Cet opérateur sert à tester si 2 conditions sont simultanément vérifiées (ou pas).
L'opérateur logique AND : &&
Exemple :
Ecrire une expression booléenne qui est vrai si la valeur de la variable entière toto est strictement comprise entre 0 et 12
// Déclaration des variables
boolean exp;
int toto;
// Instructions du programme
std::cin >> toto ; // saisie clavier d'un entier dans toto
exp = (toto > 0) && (toto < 12);// vrai si toto est entre 0 et 12, faux sinonL'opérateur logique OR : ||
| A | B | A || B |
| true | true | true |
| true | false | true |
| false | true | true |
| false | false | false |
Le résultat est true ssi au moins l'une des deux opérandes A ou B vaut true.
Cet opérateur sert à tester si au moins 1 condition sur 2 est vérifiée (ou pas).
L'opérateur logique OR : ||
Exemple :
Ecrire une expression booléenne valant vrai si la valeur de la variable entière toto n'est pas comprise entre 0 et 12.
// Déclaration des variables
boolean exp;
int toto;
// Instructions du programme
std::cin >> toto ; // saisie clavier d'un entier dans toto
exp = (toto < 0) || (toto > 12);// vrai si toto n'est pas entre 0 et 12, faux sinonPriorité entre l'opérateur AND et OR
Dans une expression impliquant l'opérateur AND et l'opérateur OR, AND est prioritaire sur OR.
A && B || C est équivalent à (A && B) || CNotons au passage :
- la priorité entre AND et OR est analogue à la priorité de la mutliplication sur l'addition pour des nombres. D'ailleurs, AND est aussi appelé "multiplication logique" et OR "addition logique".
- même si elles sont optionnelles, utilisez des parenthèses pour expliciter l'ordre dans lequel sont évalués les termes d'une expression logique. Cela facilite sa compréhension.
L'opérateur logique NOT : !
| A | !A |
| true | false |
| false | true |
C'est un opérateur "unaire" (il s'applique à une valeur booléenne et non deux comme AND et OR).
Il exprime la négation, l'opposé de l'expression logique.
L'opérateur logique NOT : !
Exemple :
Ecrire une expression booléenne
valant vrai si la valeur de la variable entière toto n'est pas comprise
entre 0 et 12. Cette fois, proposez une solution qui fait bon usage de
l'opérateur NOT.
// Déclaration des variables
boolean exp;
int toto;
// Instructions du programme
std::cin >> toto ; // saisie clavier d'un entier dans toto
exp = !( (toto > 0) && (toto < 12) );// vrai si toto n'est pas entre 0 et 12, faux sinonExercice
Les opérateurs logiques permettent de combiner différents tests
simples afin de construire des expressions plus élaborées.
Ecrire une expression booléenne qui vaut true si la valeur entière contenue dans une variable toto est paire et strictement supérieur à 100.
// Déclaration des variables
boolean exp;
int toto;
// Instructions du programme
std::cin >> toto ; // saisie clavier d'un entier dans toto
exp = (toto%2 == 0) && (toto > 100);// vrai si toto est paire et plus grand que 100L'opérateur logique NAND
| A | B | A NAND B |
| true | true | false |
| true | false | true |
| false | true | true |
| false | false | true |
NAND est la contraction de NOT AND. Autrement dit :
- Note : il n'y a pas de syntaxe spécifique à cet opérateur en C++, on utilisera donc l'écriture !(A && B)
L'opérateur logique NOR
| A | B | A NOR B |
| true | true | false |
| true | false | false |
| false | true | false |
| false | false | true |
De même, NOR est la contraction de NOT OR. Autrement dit :
- Note : pas de syntaxe C++ spécifique non plus. On utilisera donc l'écriture !(A || B)
A retenir concernant NAND et NOR
Ces opérateurs soint moins courants puisqu'ils ne permettent pas d'exprimer plus que la combinaison de NOT, AND et OR.
Mais leurs tables de vérité permettent de déduire deux relations intéressantes :
NOT(A OR B) est équivalent à NOT(A) AND NOT(B)
Notons au passage :
- Ces deux relations sont appelées les lois de De Morgan, en référence à Auguste De Morgan.
- elles sont pratiques pour développer ou factoriser les expressions logiques afin d'en simplifier l'écriture.
Priorité entre opérateurs
Une expression comporte souvent plusieurs types d'opérateur. La priorité entre ces opérateurs est importante pour comprendre comment la machine évalue une expression :
- opérateurs arithmétiques
- opérateurs de comparaison
- opérateurs logiques
// Déclaration des variables
boolean exp;
int toto;
// Instructions du programme
std::cin >> toto ; // saisie clavier d'un entier dans toto
exp = toto + 4 < 12 && toto - 4 > 0;
// ou : exp = ( (toto+4) < 12 ) && ( (toto-4) > 0 )- Bases de l'Algorithmique
- Introduction
- Types, variables et opérateurs
- Instructions structurées
- Les tableaux
- Tableaux unidimensionnels
- Tableaux bidimensionnels
- Les fonctions
Les instructions structurées
Qu'avons nous appris ?
- Lire/écrire des données dans la mémoire de la machine
- Lui ordonner de faire des calculs (avec des opérateurs)
Le tout s'effectue séquentiellement. Les instructions structurées vont nous permettre :
- Définir des blocs d'instructions
- Casser l'exécution séquentielle d'un algorithme
Les instructions conditionnelles
Elles permettent d'exécuter un bloc d'instructions si et seulement si une condition choisie est satisfaite.
Supposons par exemple devoir diviser un nombre a par un nombre b. La division par zéro étant impossible, ce calcul ne peut être réalisé que si b est différent de 0.
Bloc Conditionnel :
"Si (expression booléenne) alors" ?

Instruction conditionnelle simple
Syntaxe :
if ( /* expression booléenne */ ) // l'expression se place entre parenthèses
{ // l'accolade ouvrante indique le début du bloc d'instructions
/* bloc d'instructions */
} // l'accolade fermante indique la fin du bloc d'instructionsPrincipe :
- si l'expression vaut true, les instructions du bloc seront exécutées
- si l'expression vaut false, le bloc est ignoré
- Attention, le si.... n'est pas une instruction : pas de ; à la fin
Instruction conditionnelle simple
Revenons à la problématique suivante : Comment dire à la machine "Si b est différent de 0, alors calcule a/b" ?
// Déclaration des variables
int a, b, division;
// Instructions du programme
std::cout << "Saisir les valeurs de a et de b " << std::endl;
std::cin >> a >> b ;
if ( b != 0 )
{
division = a / b;
std::cout << "La division de a par b est " << division << std::endl;
}Instruction conditionnelle complète
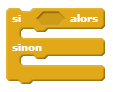
Principe :
- si l'expression vaut true, les instructions du premier bloc seront exécutées
- sinon ce sont les instructions du second bloc qu'on exécute
Instruction conditionnelle complète
Syntaxe :
if ( /* expression booléenne */ )
{ // l'accolade ouvrante
/* bloc d'instructions à exécuter
si l'expression booléenne vaut true */
} // l'accolade fermante
else
{
/* autre bloc d'instructions à exécuter
si l'expression booléenne vaut false */
}- si l'expression vaut true, les instructions du premier bloc seront exécutées
- sinon ce sont les instructions du second bloc qu'on exécute
Instruction conditionnelle complète
Exercice :Même exercice que le précédent mais on vous demande de faire afficher "division par zéro interdite" si le cas se produit.
// Déclaration des variables
int a, b, division;
// Instructions du programme
std::cout << "Saisir les valeurs de a et de b " << std::endl;
std::cin >> a >> b ;
if ( b != 0 )
{
division = a / b;
std::cout << " La division de " << a << " par " << b << " est égale à " << division << std::endl;
}
else
{
std::cout << " La division par zéro est interdite" << std::endl;
}
Instructions conditionnelles
imbriquées
Un bloc d'instructions peut contenir d'autres instructions conditionnelles.
if ( ... )
{
if (...)
{
...
}
else
{
...
}
}
else
{
if (...)
{
...
}
else
{
...
}
}
Instructions conditionnelles
imbriquées
Exercice :
Ecrire un algorithme qui demande à l'utilisateur de saisir un nombre entre 1 et 7
On ne demande pas de vérifier que le nombre entier saisi est bien compris entre 1 et 7, on supposera que c'esr toujours le cas.
Puis en fonction du nombre saisi, le programme affiche le nom du jour de la semaine correspondant. Par exemple "lundi" pour 1, "mardi" pour 2 etc...
Instructions conditionnelles
imbriquées
Solution :
// Déclaration des variables
int jour;
// Instructions du programme
std::cout << "Saisir un nombre entier entre 1 et 7 \n";
std::cin >> jour ;
if ( jour == 1 )
std::cout << "lundi";
else
{
if ( jour==2 )
std::cout <<"mardi";
else
{
if ( jour==3 )
std::cout <<"mercredi";
else
{
if ( jour==4 )
std::cout <<"jeudi";
else
{
if ( jour==5 )
std::cout <<"vendredi";
else
{
if ( jour==6 )
std::cout <<"samedi";
else
std::cout <<"dimanche";
}
}
}
}
}Instructions conditionnelles
imbriquées
Notons au passage :
- pour un block qui ne contient qu'une seule instruction, on n'est pas obligé de le délimiter par une accolade ouvrante et une accolade fermante.
- le grand nombre d'imbrications rend le code moins évident à lire. Ce qui le garde lisible, c'est l'indentation ! Chaque fois que l'on commence un nouveau bloc, on augmente la marge d'une tabulation ou de 4 espaces. C'est primordial pour la lisibilité et donc la compréhension du code.
- Vous ne me croyez ? Voyez plutôt la diapo suivante qui vous présente le même code mais non indenté.
Instructions conditionnelles
imbriquées
/* Même solution mais non indenté...
Notez que je ne corrigerai pas vos programmes s'ils sont mal indentés. */
// Déclaration des variables
int jour;
// Instructions du programme
std::cout << "Saisir un nombre entier entre 1 et 7 \n";
std::cin >> jour ;
if ( jour == 1 )
std::cout << "lundi";
else
{
if ( jour==2 )
std::cout <<"mardi";
else
{
if ( jour==3 )
std::cout <<"mercredi";
else
{
if ( jour==4 )
std::cout <<"jeudi";
else
{
if ( jour==5 )
std::cout <<"vendredi";
else
{
if ( jour==6 )
std::cout <<"samedi";
else
std::cout <<"dimanche";
}
}
}
}
}Instructions conditionnelles
imbriquées
Dans le cas d'un "Si, sinon si, sinon si, .... sinon", et seulement dans ce cas, on peut utiliser la syntaxe équivalente suivante pour une meilleure lisibilité :
if (...)
{
...
}
else if (...)
{
...
}
else if (...)
{
...
}
...
else
{
...
}Instructions conditionnelles
à choix multiple
L'exercice précédent peut s'écrire d'une manière plus efficace
En utilisant l'instruction switch
Syntaxe :
switch (variable)
{
case valeur1 :
instruction1;
break;
case valeur2,valeur3 :
instruction2;
instruction2bis;
break;
.
.
.
default:
instructionDefaut;
break;
}
if (variable == valeur1)
instruction1;
else if (variable == valeur1 || variable == valeur2)
{
instruction2;
instruction2bis;
}
.
.
.
else {
instructionDefaut;
}
}Instructions conditionnelles
à choix multiple
L'exercice précédent peut s'écrire :
// Déclaration des variables
int jour;
// Instructions du programme
std::cout << "Saisir un nombre entier entre 1 et 7 \n";
std::cin >> jour ;
switch (jour)
{
case 1:
std::cout << "Lundi";
break;
case 2:
std::cout << "Mardi";
break;
case 3:
std::cout << "Mercredi";
break;
case 4:
std::cout << "Jeudi";
break;
case 5:
std::cout << "Vendredi";
break;
case 6:
std::cout << "Samedi";
break;
case 7:
std::cout << "Dimanche";
break;
default:
std::cout << "Erreur";
break;
}
Instructions conditionnelles
à choix multiple
Précisions sur l'instruction switch
- Ne fonctionne qu'avec des variables de type int et char
- En C++, le système, après avoir
reconnu une valeur, continue a effectuer les instructions suivantes - L'instruction break sert a briser l'execution du programme et a passer directement a l'instruction suivant l'accolade fermante
- L'instruction break est donc indispensable lors d'un switch
Instructions de répétition :
Les boucles
Nous sommes encore limités...Par exemple, pouvez-vous écrire un programme qui affiche 6 fois la chaîne "Bonjour" ?
On ne vous fera pas l'offense de penser le contraire ! Mais pouvez vous en écrire un qui affiche 1 million de fois la chaîne "Bonjour" ? Surtout en avez vous le temps (et l'envie !) ?
Il faut utiliser l' instruction :

La boucle for
Syntaxe :
int i; // déclaration d'une variable entière qui sera l'indice de la boucle
for ( i=n; i<=m; i++ ) // n et m sont deux entiers
{
/* bloc d'instructions à répéter */
}- la boucle for permet de répéter le bloc d'instructions qui la suit un certain nombre de fois
- le nombre de répétitions (ou tours de boucle) est choisi grâce à l'indice de boucle, ici la variable i. L'indice de boucle est le "compteur" de la boucle.
- i=n; fixe la valeur initiale de i, la variable "compteur"
- i<=m; fixe la valeur maximale de i. La boucle tourne tant que i<=m est vrai
- i++ est la contraction de i=i+1. Indique que i augmente de 1 à chaque tour
La boucle for
Exercice :Ecrire un algorithme qui affiche 1 million de fois "Bonjour".
int i;
for ( i=1; i<=1000000; i++ )
{
std::cout << "Bonjour" << std::endl;
}- i vaut 1, donc i<=1000000 est vrai, donc le bloc est exécuté une première fois et i augmente de 1
- i vaut 2, donc i<=1000000 est vrai, donc le bloc est exécuté une seconde fois et i augmente de 1
- ...
- i vaut 1 million, donc i<=1000000 est vrai, donc le bloc est exécuté une millionième fois et i augmente de 1
- i<1000000 est maintenant faux ! La boucle s'arrête et le programme continue
La boucle for
Exercice :Variante : Ecrire un algorithme qui affiche "Bonjour" Autant de fois qu'un nombre entier préalablement saisi par l'utilisateur.
int i, nb;
std::cout << "Saisir le nombre de bonjour " ;
std::cin >> nb;
std::cout << std::endl;
for ( i=1; i<=nb; i++ )
std::cout << "Bonjour" << std::endl;
std::cout << "Saisir le nombre de bonjour " ;
std::cin >> nb;
std::cout << std::endl;
for ( i=0; i<nb; i++ )
std::cout << "Bonjour" << std::endl;
Notes :
- les accolades délimitant le bloc sont optionnelles s'il ne contient qu'une instruction
- ces deux solutions sont équivalentes, le nombre de tour est toujours le même.
La boucle for
Exercice :Ecrire un algorithme qui demande la saisie d'un nombre entier n et qui affiche ensuite tous les nombres de 1 à n.
int i, n;
std::cout << "Saisir un entier positif " ;
std::cin >> nb;
for ( i=1; i<=n; i++ )
std::cout << i << " ";
Note :
- utiliser l'indice de boucle dans le bloc de la boucle est très fréquent et très pratique !
La boucle for
Quand l'utiliser ?Utiliser une boucle for suppose de connaître par avance le nombre de tours à effectuer.
Limitation
On peut avoir besoin de répéter des instructions sans pour autant savoir combien de fois par avance !
Les instructions de répétition
ExempleUn programme doit poser une question à l'utilisateur qui doit y répondre par oui ou par non en frappant sur le caractère 'o' ou 'n'. Dans le cas contraire la question doit lui être posée à nouveau.
Ici on ne peut pas prédire le nombre de tentatives dont l'utilisateur aura besoin. Par conséquent une boucle for est inutilisable. Mais ce n'est pas le seule type de boucle qui existe :

Attention, l'instruction scratch est "inversée" par rapport au C++ !
La boucle while
Syntaxe :
while ( /* expression booléenne */ )
{
/* bloc d'instructions à répéter */
} - la boucle while permet de répéter le bloc d'instructions qui la suit jusqu'à ce qu'une expression booléenne devienne fausse
- lorsque l'expression devient fausse, la boucle s'arrête et le programme continue
- attention, il faut être certain que l'expression booléenne puisse devenir fausse à un moment donné si l'on ne veut pas rester "coincé" dans la boucle
La boucle while
Exercice :Poser la question "Avez-vous compris ?" jusqu'à ce que l'utilisateur réponde oui en frappant sur la lettre 'o'.
char reponse='n';
while ( reponse!='o' )
{
std::cout << "Avez-vous compris ?" ;
std::cin >> reponse;
} Notes :
- Quelle est l'importance de l'initialisation de la variable reponse ici ?
- Que se passera-t-il si reponse est initialisée avec le caractère 'o' ?
La boucle do while
Syntaxe :
do
{
/* bloc d'instructions à répéter */
}
while ( /* expression booléenne */ );- comme la boucle while, sauf que le bloc est forcément exécuté au moins une fois !
- attention à ne pas oublier le point-virgule dans ce cas
La boucle do while
Exercice :Poser à l'utilisateur la question "Avez-vous compris ?" jusqu'à ce qu'il réponde oui en frappant sur la lettre 'o'.
char reponse;
do
{
std::cout << "Avez-vous compris ?" ;
std::cin >> reponse;
}
while ( reponse!='o' ); Notes :
- même exercice que précédemment mais une solution avec une boucle do while
- reponse n'est pas initialisée à sa déclaration, est-ce toujours un problème ?
Les boucles : Exercice
Le jeu du nombre mystèreLe but est de faire deviner à l'utilisateur un nombre entier choisi aléatoirement entre 0 et 99. A chaque proposition du joueur, la machine indique si le nombre proposé est plus petit ou plus grand que le nombre à deviner. Lorsque le bon nombre est trouvé, la machine affiche un message de félicitations.
On utilisera l'instruction rand() qui génère aléatoirement (ou presque) un nombre compris entre 0 (inclus) et RAND_MAX(exclu).
Par exemple float nb_alea = (float)rand() / (1.0 + RAND_MAX); initalisera nb_alea avec une valeur entre 0 et 1.0.
Aussi int adeviner = (int) (100.0 * rand() / (1.0 + RAND_MAX)); initialisera adeviner avec une valeur entre 0 et 99.
L'écriture (int)(...) commande à la machine de convertir l'expression entre parenthèse en nombre entier. Dans le cas d'un nombre réel, seule la partie entière sera conservée. Par exemple (int)( 73.234 ) donnera 73.
Les boucles : Exercice
Le jeu du nombre mystère
int proposition, adeviner = (int)(100.0 * rand()/(1.0 + MAX_RAND));
do
{
std::cout << "Proposer un nombre entre 0 et 99 :"<< std::endl;
std::cin >> proposition;
if ( proposition < adeviner )
std::cout << "Trop petit !" << std::endl;
else if ( proposition > adeviner )
std::cout << "Trop grand"<< std::endl;
else
std::cout << "Félicitations ! C'était bien " << adeviner<< std::endl;
}
while ( proposition != adeviner ); Notons au passage :
- quelle est la façon la plus rapide pour gagner ? Enumérer les nombres de 0 à 99 ? Ou bien avez-vous une meilleure idée ?
- la stratégie à laquelle vous avez probablement pensée très rapidement s'appelle la recherche par dichotomie ! Un grand classique en algorithmique !
Les boucles imbriquées
PrincipeLe bloc d'instructions d'une boucle peut contenir d'autres boucles bien sûr ! On parle alors de boucles imbriquées
Attention
Des boucles imbriquées ne sont pas indépendantes les unes des autres. De fait, il faudra faire attention à utiliser un indice de boucle différent pour chacune !
Les boucles imbriquées
ExerciceAfficher à l'écran les tables de multiplication de 1 à 10. Au besoin, afficher d'abord la table de 1, puis modifier votre code pour afficher les tables de 1 à 10.
int i, j;
for( i=1; i<=10; i++)
{
std::cout << "Table de multiplication de " << i << std::endl;
for( j=1; j<=10; j++)
{
std::cout << i << " x " << j << " = " << i*j << std::endl;
}
}
Erreurs :
Les grands classiques
L'infini existe, et vous allez vous y perdre !
int x;
do
{
x = 1;
x = x + 1;
}
while( x<10 );
- le risque avec une boucle, c'est de ne jamais en sortir
- pour en savoir un peu plus, clic
- Bases de l'Algorithmique
- Introduction
- Types, variables et opérateurs
- Instructions structurées
- Les tableaux
- Tableaux unidimensionnels
- Tableaux bidimensionnels
- Les fonctions
Limites des données élémentaires
Comment regrouper des données de même type ?Supposons devoir saisir les noms d'une promotion d'étudiants. En l'état de nos connaissance, il faut :
- déclarer une variable de type
stringpar étudiant - affecter chaque variable une par une
Oui mais...
De la sorte, on ne matérialise pas du tout l'appartenance à un même ensemble (la promotion)
Limites des données élémentaires
ExempleOn souhaite saisir 6 notes et les afficher de la plus petite à la plus grande
C'est faisable mais...
... ce n'est pas extensible. Avec 16 notes il faudra 10 variables de plus et le code pour les ordonner va très vite devenir illisible. De plus si on ne connait pas par avance le nombre de notes à saisir, on ne sait pas faire.
Limites des données élémentaires
L'origine de ces problèmes, c'est notre incapacité à définir un ensemble de données homogènes
Solution
Regrouper des éléments de même type au sein d'une collection d'éléments. Pouvoir parcourir cette collection et si besoin accéder facilement à chaque élément.
Tableaux unidimensionels
DescriptionUn tableau regroupe un nombre n d'éléments de même type. Chaque case du tableau est identifiée par un indice allant de 0 jusqu'à n-1. n est aussi appelé la taille du tableau
Illustration

Tableaux unidimensionels
Déclaration d'un tableau
// déclaration d'un tableau d'entiers de taille 8
int int_tab[8];
// déclaration d'un tableau de caractères de taille 1024
char car_tab[1024] ;
// déclaration d'un tableau de booléens de taille 256
bool b_tab[256] ;
// déclaration d'un tableau de 28 chaînes
string chaine_tab[25] ;- De manière générale, la syntaxe est : nom_du_type nom_du_tableau[taille (constante)];
- côté machine, le type des éléments du tableau lui permet de définir combien d'octets occupera une case
- ensuite, fixer la taille du tableau à
nlui permet de réservernplaces/cases consécutives en mémoire pour y ranger des valeurs du type indiqué - c'est important car c'est parce que les éléments se suivent en mémoire que l'on peut les manipuler par leur indice de tableau
- Les réservations sont ici faites de manière statique, c.a.d. lors de la phase de compilation
Tableaux unidimensionels
(Apparté) Dimensionner un tableau dynamiquement
// déclaration d'un tableau d'entiers de taille 8
int* int_tab = new int[8]:
// déclaration d'un tableau de 1024 caractères
char* car_tab = new char[1024];
// déclaration d'un tableau de booléens de taille 256
bool* b_tab = new boolean[256];
// déclaration d'un tableau de 28 chaînes
string* chaine_tab= new string[28];
- Les reservations de places sont ici crées de manière dynamique (lors de l'éxecution du programme)
Tableaux unidimensionels
Accès aux éléments d'un tableauPour accéder (en lecture ou écriture) à un élément dans un tableau, on utilise l'indice de la case qui le contient.
Syntaxe : nom_du_tableau[ indice_de_la case ]
int sum;
int tab[4]; // tableau de taille 4
tab[0] = 10; // affecte 10 à la case d'indice 0
tab[1] = 2; // affecte 2 à la case d'indice 1
tab[2] = 23; // affecte 23 à la case d'indice 2
tab[3] = 99; // affecte 99 à la case d'indice 3
sum = tab[0] + tab[3]; // sum vaut 109- Attention, l'indice doit obligatoirement être compris entre
0(inclus) et la taille du tableau (exclue)
Tableaux unidimensionels
ExerciceEcrire un algorithme qui initialise toutes les cases d'un tableau de 1024 entiers à -1
int i;
int tab[1024];
for(i=0; i<1024; i++)
tab[i] = -1;Même question mais en remplissant chaque case avec les entiers de 1 à 1024
int i;
int tab[1024];
for(i=0; i<1024; i++)
tab[i] = i+1;- Boucles et tableaux font bon ménage. Utiliser l'indice d'une boucle
forpour parcourir les indices d'un tableau est incontournable
Tableaux unidimensionels
ExerciceEcrire un algorithme pour saisir 28 notes dans un tableau.
const int nb_notes = 28;
double notes[nb_notes]; // le tableau
int i; // indice de boucle pour le parcours du tableau
std::cout << "Saisir les " << nb_notes << " notes\n";
// saisie des notes dans le tableau
for(i=0; i<nb_notes; i++)
std::cin >> notes[i] ;- On utilise ici la constante nb_notes pour conserver la longueur du tableau
- Cela évite de modifier à la main le programme en entier si on souhaite changer la taille du tableau
Tableaux unidimensionels
ExerciceModifier le programme précédent pour en plus calculer la moyenne des 28 notes
const int nb_notes = 28;
double notes[nb_notes]; // le tableau
int i; // indice de boucle pour le parcours du tableau
double avg = 0.0; // pour calculer la moyenne
std::cout << "Saisir les " << nb_notes << " notes\n";
// saisie des notes dans le tableau
for(i=0; i<nb_notes; i++)
std::cin >> notes[i] ;
// calcul de la somme de toutes les notes
for(i=0; i<nb_notes; i++)
avg = avg + notes[i];
std::cout << " La moyenne est : " << avg/(float)nb_notes << std::endl;- chaque tour de boucle ajoute à
avgune note de plus - on pourrait n'utiliser qu'une boucle en cumulant les notes au fur et à mesure ou elles sont saisies
Tableaux unidimensionels
ExercicePour finir, faites en sorte de demander à l'utilisateur le nombre de notes à saisir pour ne plus être restreint à 28 notes
double* notes; // le tableau non dimensionné
int i; // indice de boucle pour le parcours du tableau
int nb_notes; // nombre de notes à saisir
double avg = 0.0; // pour calculer la moyenne
std::cout << "Combien de notre à saisir ?" << std::endl;
std::cin >> nb_notes ;
notes = new double[ nb_notes ];
std::cout << "Saisir les " << nb_notes << " notes\n";
// saisie des notes dans le tableau
for(i=0; i<nb_notes; i++)
std::cin >> notes[i];
// calcul de la somme de toutes les notes
for(i=0; i<nb_notes; i++)
avg = avg + notes[i];
std::cout << "La moyenne est : " << avg/(float)nb_notes << std::endl;Tableaux unidimensionels
Limite des tableaux unidimensionelsLes données sont souvent structurées. Par exemple un chevalet de scrabble possède une structure qui correspond à un tableau 1D. Mais le plateau de jeu du scrabble possède une structure difficile à représenter avec un tableau 1D.
Autre exemple : une image bitmap possède une structure 2D. Nous aurons du mal à la représenter avec un tableau 1D. Car la dimension de la structure des données ne correspond pas !
Tableaux unidimensionels
MoralitéPour bien représenter des données, pouvoir les manipuler efficacement, il faut utiliser des structures capables de reproduirent l'organisation intrinsèque de ces données.
- Les tableaux
- Introduction
- Types, variables et opérateurs
- Instructions structurées
- Les tableaux
- Tableaux unidimensionnels
- Tableaux bidimensionnels
- Les fonctions
Tableaux bidimensionels
DescriptionUn tableau 2D est une structure de grille caractérisée par son nombre l de lignes et sont nombre c de colonnes, respectivement numérotées de 0 à l-1 et de 0 à c-1.
Un tableau 2D stocke l x c éléments de même type. L'emplacement d'un élément est identifié par les indices de ligne et de colonne à l'intersection desquelles il se trouve.
Tableaux bidimensionels
Illustration
Tableaux bidimensionels
Déclaration d'un tableau 2D
// déclaration d'un tableau 2D d'entiers
int int_tab[10][10];
// déclaration d'un tableau 2D de caractères
char car_tab[10][10];
// déclaration d'un tableau 2D de booléens
bool b_tab[10][10];
// déclaration d'un tableau 2D de chaînes
string chaine_tab[10][10];
- De manière générale, la syntaxe est : nom_du_type nom_du_tableau[ligne][colonne];
- Attention, définir la taille des tableaux de manière dynamique requiert en C++ une mécanique plus complexe. Nous nous contenterons pour ce semestre de tableaux 2D statiques (de taille connue lors de la compilation)
Tableaux bidimensionels
Notez au passage
// type entier
int value;
// type tableau 1D de valeurs de type entier
int tab1D[l] ;
// type tableau 2D de valeurs de type entier
int tab2D[l][c];
// valable quelque soit le type de départ bien sûr
// type tableau 3D de valeurs de type entier !
int tab3D[l][c][z];
// et ainsi de suite... mais on s'arrêtera à la 2D.
Tableaux bidimensionels
Accès aux éléments d'un tableau 2DPour accéder à un élément dans un tableau 2D, on utilise l'indice de la ligne et de la colonne qui identifient la case qui le contient. Syntaxe :
nom_du_tableau[ indice_de_la_ligne ][indice_de_la_colonne]
int sum;
int tab[4][8]; // tableau 2D de 4 lignes et 8 colonnes
tab[0][7] = 10; // affecte 10 à la case de coordonnées (0, 7)
tab[1][0] = 2; // affecte 2 à la case de coordonnées (1, 0)
tab[3][3] = 99; // affecte 99 à la case de coordonnées (3, 3)
sum = tab[0][7] + tab[3][3]; // sum vaut 109
- Attention, les indices de lignes et colonnes doivent obligatoirement être compris entre
0(inclus) et respectivement le nombre de lignes (exclu) et le nombre de colonnes (exclu)
Tableaux bidimensionnels
ExerciceEcrire un programme qui permet de saisir case par case le contenu d'un tableau 2D représentant les notes dans 12 modules obtenu par 28 étudiants
int l, c;
double notes[28][12];
for( l=0; l<28; l++)
{
for( c=0; c<12; c++)
{
std::cout << "Note de l'étudiant" << l << " pour le module " << c << std::endl;
std::cin >> notes[l][c] ;
}
}
- Bases de l'Algorithmique
- Introduction
- Types, variables et opérateurs
- Instructions structurées
- Les tableaux
- Tableaux unidimensionnels
- Tableaux bidimensionnels
- Les fonctions
L'analyse globale
C'est à dire ?L'analyse globale est une approche qui consiste à appréhender un problème dans sa totalité pour écrire un programme qui va le résoudre
Pas toujours envisageable...
Si le problème devient complexe, il devient aussi difficile de l'appréhender dans sa globalité :
- calculer la somme des nombres de 1 à n : ça va.
- réaliser un simulateur de formule 1 : moins évident.
Notez que...
Ce n'est pas spécifique à l'algorithmique !- cuire des pâtes / feuilleté de tartare et émultion de foie gras
- faire un avion en papier / faire une fusée Ariane 5
La solution : diviser pour mieux règner
Un problème trop complexe doit être décomposé en sous problèmes moins complexes.
L'analyse descendante
Subdiviser un problème en sous-problèmes de sorte que- chaque problème est indépendant des autres
- chaque problème est plus simple à résoudre
Un sous-problème peut lui-même être re-subdivisé
- on descend à un niveau d'analyse inférieur
Fonction
Définition- une fonction est un sous-programme
- elle possède ses propres entrées et sortie
- on peut y faire appel chaque fois qu'on en a besoin
Intérêts d'une fonction
- décomposer un programme complexe en sous-programmes élémentaires
- réutiliser le code !
- structurer et clarifier le code
Analyse descendante et fonctions
Analyse descendante- Problème global
- sous-problèmes
- sous-problèmes
Décomposition d'un programme
- Fonction principale (main)
- fonctions
- fonctions
Communiquer avec des fonctions
QuestionUne fonction traite un problème et donc en général, elle aura besoin qu'on lui fournisse des données à traiter. Eventuellement nous aurons aussi besoin de récupérer le résultat de ce traitement.
Notion de paramètre et valeur de retour
Ces notions permettent de communiquer avec une fonction
- les paramètres permettent de transmettre des données existantes à une fonctions
- la valeur de retour permet de récupérer une nouvelle donnée créée par une fonction
- Bases de l'Algorithmique
- Introduction
- Types, variables et opérateurs
- Instructions structurées
- Les tableaux
- Tableaux unidimensionnels
- Tableaux bidimensionnels
- Les fonctions
Déclarer une fonction
C'est-à-dire ?Déclarer une fonction c'est :
- l'identifier par un nom
- identifier les types des données dont elle a besoin (ses paramètres)
- identifier le type de donnée qu'elle produit (sa valeur de retour)
- écrire le code qu'elle réalisera si on l'appelle
Notez bien
- une fonction non déclarée n'existe pas
- une fonction jamais appelée ne sert à rien
Déclarer une fonction
Syntaxertype function_name ( ptype1 pname1, ptype2 pname2...)
{
// code de la fonction
}
function_nameest le nom de la fonctionrtypeest le type de la valeur retournée par la fonctionptype1, ptype2...sont les types ses paramètrespname1, pname2...sont les noms ses paramètres
Déclarer et appeler une fonction
Fonction sans paramètre, sans valeur de retour
// fonction sans paramètre, sans valeur de retour (void = rien)
void doSomething()
{
// ici le code de la fonction doSomething
...
}
// fonction principale main (elle aussi sans paramètre mais avec une valeur de retour)
int main()
{
// appel à la fonction doSomething depuis la fonction main
doSomething();
}
voidsignifie "rien" : rien n'est retourné par la fonctiondoSomethingest la fonction appelée,mainest la fonction appelante- la machine exécute toujours en premier le code de la fonction principale.
- l'appel à
doSomethingprovoque l'exécution de son code. - puis l'exécution du code de la fonction
mainse poursuit. - En C/C++, la fonction principale retourne un entier (un code d'erreur/execution)
Déclarer et appeler une fonction
ExerciceEcrire une fonction qui affiche un smiley dessiné en ASCII. Puis écrire un programme qui permet de l'afficher autant de fois que l'utilisateur le souhaite.
void smiley()
{
std::cout << " (\___/) " << std::endl;
std::cout << " (='.'=) "<< std::endl;
std::cout << " (¨)_(¨) "<< std::endl;
}
void main()
{
int i, nb;
std::cout << "Nombre de fois : " << std::endl;
std::cin >> nb;
for(i=1; i<=nb; i++)
smiley();
}
Déclarer et appeler une fonction
ExerciceEcrire une fonction qui affiche la table de multiplication par 7 et une autre fonction qui affiche la table de 5. Faites un programme qui affiche ces 2 tables.
void tableDe5()
{
int i;
for(i=0; i<=10; i++){
std::cout << "5 x " << i << " = " << 5*i << std::endl;
}
}
void tableDe7()
{
int i;
for(i=0; i<=10; i++){
std::cout << "7 x " << i << " = " << 7*i << std::endl;
}
}
int main()
{
tableDe5();
tableDe7();
}
Portée d'une variable locale
Dans l'exercice précédent, deux variables i sont déclarées :
- l'une dans
tableDe5 - l'autre dans
tableDe7
Elles sont sans aucun rapport !
L'existence d'une variable déclarée à l'intérieur d'une fonction est limitée à cette fonction. On dit que la variable est locale à la fonction et que sa portée est restreinte à la fonction.
Il y a la variable i de la fonction tableDe5 et la variable i de la fonction tableDe7.
Une fonction n'a aucune connaissance des variables d'une autre fonction et réciproquement.
Déclarer et appeler une fonction
Fonction avec paramètre(s), sans valeur de retour
// fonction avec un paramètre de type int nommé toto
void doSomething( int toto )
{
// code de la fonction doSomething utilisant toto (sa valeur)
}
// fonction principale main (elle aussi sans paramètre ni valeur de retour)
int main()
{
// appel à la fonction doSomething en transmettant une valeur entière
doSomething(10);
}
- le paramètre
totopermet de transmettre une valeur entière à la fonction lorsqu'on l'appelle doSomething(10)signifie que le code de la fonction s'exécutera avectotovalant 10
Déclarer et appeler une fonction
ExerciceEcrire une fonction pour chaque table de multiplication est pénible. A la place, écrire plutôt une fonction qui affiche la table de multiplication de l'entier fourni en paramètre.
void tableDe( int n )
{
int i;
for(i=0; i<=10; i++)
std::cout << n <<" x " << i << " = " << n*i << std::endl;
}
int main()
{
int nb ;
std::cout << "Quelle table voulez vous ?" << std::endl;
std::cin >> nb ;
tableDe(nb);
}
Fonctionnement d'un paramètre
- Le paramètre permet à la fonction appelante de transmettre une donnée à la fonction appelée
- Le type de la donnée transmise doit correspondre au type du paramètre
Un paramètre peut être vu comme une variable spéciale qui sert de zone d'échange entre la fonction appelante et la fonction appelée.
Dans l'exercice précédent, lors de l'appel tableDe(nb), la valeur de la variable nb est recopiée dans le paramètre n. De fait tableDe s'exécute pour la valeur saisie par l'utilisateur.
Une conséquence non négligeable pour la suite, c'est qu'une fonction n'utilise jamais les valeurs qu'on lui transmet, mais des copies de ces valeurs.
Déclarer et appeler une fonction
ExerciceEcrire une fonction possédant 2 paramètres, un de type String l'autre de type char. La fonction affichera le mot transmis via le premier paramètre mais encadré d'un rectangle dessiné avec le caractère transmis via le second paramètre.
void frame( string word, char c, int longueur ) // longeur du cadre = taille du mot + 2
{
int i;
for(i=1; i<=longueur; i++) // haut du cadre
std::cout << c;
std::cout << std::endl; // retour à la ligne
std::cout << c << word << c << std::endl; // le mot encadré de 2 caractères c
for(i=1; i<=longueur; i++) // bas du cadre
std::cout << c;
std::cout << std::endl;
}
void main()
{
frame("Hello World !", '*', 15);
}
Lorsqu'une fonction présente plusieurs paramètres, l'ordre dans lequel on transmet les données doit être cohérent avec l'ordre dans lequel les paramètres de la fonction sont déclarés.
Ici le paramètre de type string est déclaré avant le paramètre de type char donc on transmettra lors de l'appel d'abord une chaîne suivie d'un caractère et non le contraire.
Déclarer et appeler une fonction
Déclarer une fonction avec valeur de retourToute valeur générée par le code d'une fonction à une portée locale. Une valeur locale est toujours détruite à la fin de l'exécution de la fonction. A moins de la "retourner"...
// fonction qui prend en paramètre un entier et retourne un entier
int auCarre( int n )
{
int res;
res = n * n;
return res; // l'entier retourné est le carré du paramètre n
}
intavant le nom de la fonction signifie qu'elle retournera une valeur de type entier- l'instruction
returnprovoque la fin de l'appel de la fonction et le retour de la valeur qui suit - le type de la valeur retournée doit être le même que le type indiqué par le prototype de la fonction
Déclarer et appeler une fonction
Appeler une fonction avec valeur de retourUne fonction avec valeur de retour ne s'appelle pas comme une fonction sans valeur de retour. Puisque la fonction appelée retourne une valeur, il est nécessaire de récupérer cette valeur dans la fonction appelante. Il faut déclarer une variable de même type que la valeur retournée afin de l'y stocker.
// fonction qui prend en paramètre un entier et retourne un entier
int auCarre( int n )
{
int res;
res = n * n;
return res; // l'entier retourné est le carré du paramètre n
}
// fonction principale main
void main()
{
int value;
value = auCarre(4);
}
- l'évaluation par la machine de l'appel
auCarre(4)donnera16 - et donc
16sera affecté à la variablevalue - ainsi, on a récupéré dans une variable locale de la fonction
mainune valeur initalement calculée dans une variable locale de la fonctionauCarre